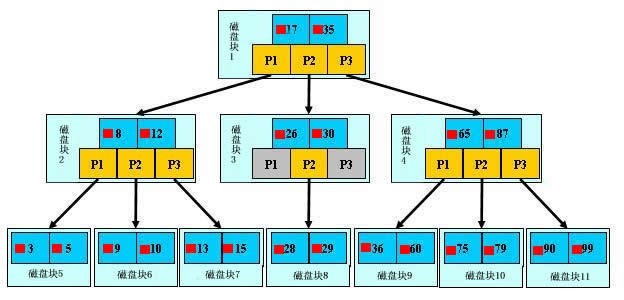
B - 树就是 B 树。m 阶 B_树满足或空，或为满足下列性质的 m 叉树：

1. 树中每个结点最多有 m 棵子树
2. 根结点在不是叶子时，至少有两棵子树
3. 除根外，所有非终端结点至少有⎡m/2⎤棵子树
4. 有 s 个子树的非叶结点具有 n = s-1 个关键字，结点的信息组织为:(n,A₀,K₁,A₁,K₂,A₂ … K_n，A_n)。这里：n 为关键字的个数，k_i（i=1,2,…,n) 为关键字，且满足 K_i 小于 K_i+1,，A_i(i=0,1,..n) 为指向子树的指针。
5. 所有的叶子结点都出现在同一层上，不带信息（可认为外部结点或失败结点）。
6. 关键字集合分布在整颗树中
7. 任何一个关键字出现且只出现在一个结点中
8. 搜索有可能在非叶子结点结束
9. 其搜索性能等价于在关键字全集内做一次二分查找
10. 只适用于随机检索，不适用于顺序检索。
11. 有结点的平衡因子都为零
12. M 阶 B - 树中含有 N 个关键字，最大深度为 log_⎡m/2⎤(n+1)/2+2

B_树中结点的插入

1. m 代表 B_树的阶，插入总发生在最低层
2. 插入后关键字个数小于等于 m-1, 完成。
3. 插入后关键字个数等于 m, 结点分裂，以中点数据为界一分为二，中点数据放到双亲结点中。这样就有可能使得双亲结点的数据个数为 m, 引起双亲结点的分裂，最坏情况下一直波及到根，引起根的分裂——B_树长高。

3 阶B_树的插入。每个结点最多 3 棵子树，2 个数据；最少 2 棵子树，1 个数据。所以 3 阶 B_树也称为 2-3 树。

B_树中结点的删除

1. 删除发生在最底层

   • 被删关键字所在结点中的关键字数目大于等于 m/2 ，直接删除。
   • 删除后结点中数据为⎡m/2⎤-2，而相邻的左（右）兄弟中数据大于⎡m/2⎤-1，此时左（右兄弟）中最大（小）的数据上移到双亲中，双亲中接（靠）在它后（前）面的数据移到被删数据的结点中
   • 其左右兄弟结点中数据都是⎡m/2⎤-1，此时和左（右）兄弟合并，合并时连同双亲中相关的关键字。此时，双亲中少了一项，因此又可能引起双亲的合并，最坏一直到根，使 B - 树降低一层。

2. 删除不在最底层

   • 在大于被删数据中选最小的代替被删数据，问题转换成在最底层的删除